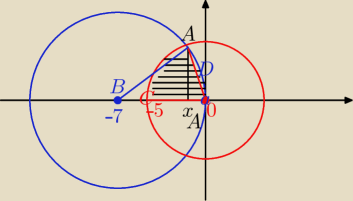
o1: S1(−7,0) r1 = 7
o2: S2(0,0) r2=5
najpierw trzeba znaleźć współrzędne punktu A(xa;ya)
szkoła:
znaleźć miarę ∡COA i miarę ∡OBA
P = pole wycinka COA + pole odcinka OAD =
pole wycinka COA + pole wycinka OBA − pole trójkąta OBA
studia:
P = −5∫xa √25−x2 dx + xa∫0 √49−(x+7)2 dx